Shunting yard algoritmus - 2. díl vlastní kalkulačky

Article in English can be found on dev.to/arxeiss/shunting-yard-parser-expression-calculator-cik

Tento článek patří do seriálu Vlastní kalkulačka s výrazy. Ostatní články seriálu:

• Lexer - 1. díl vlastní kalkulačky s výrazy
• Shunting yard algoritmus - 2. díl vlastní kalkulačky
• Evaluator AST - 3. díl vlastní kalkulačky
• Recursive descent - 4. díl vlastní kalkulačky

---

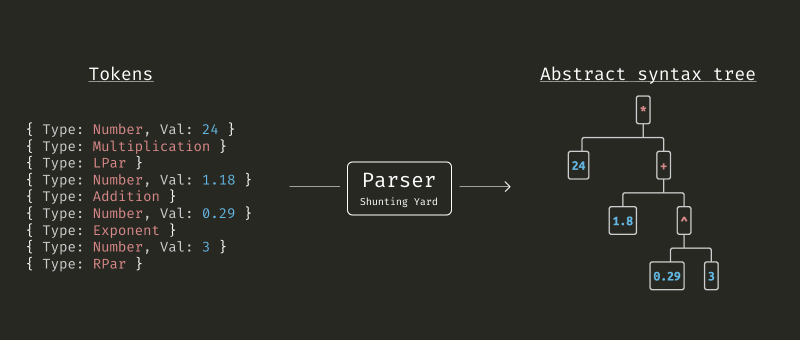
Výstupem lexikální analýzy z minulého dílu je seznam tokenů, což je jen přeformátovaný vstup. Stále není vyřešen problém závorek ani priority a asociativity operátorů. A přesně to je úkol parseru. Výstupem ale není konkrétní hodnota, nýbrž taková datová struktura, kterou lze jednoduše evaluovat. Například proměnné jsou v této struktuře stále zastoupeny pouze svým názvem. Je tedy možné evaluaci provádět i opakovaně jen s jinými vstupními hodnotami.

Zmíněný algoritmus Shunting Yard nejčastěji převádí infixovou notaci na Reverzní polskou notací, známou též jako postfixová notace. Mezi její nevýhody ale patří nemožnost spolehlivě rozeznat binární a unární operátory + a -. Nebo rozpoznat počet argumentů, které funkce přijímá, protože RPN vůbec nepoužívá závorky. Proto moje implementace převádí vstup přímo do Abstraktního syntaktického stromu, u kterého tyto problémy odpadají.

Algoritmus níže je velmi zjednodušený, kompletní implementace včetně komentářů a ukázkového kódu je opět dostupná na github.com/arxeiss/go-expression-calculator

Parser - Shunting Yard

Algoritmus Shunting Yard vynalezl E. Dijkstra a inspiroval se seřaďovacím nářadím. Protože celý průběh je pouze o přemisťování tokenů mezi vstupní frontou, zásobníkem operátorů a výstupní frontou či zásobníkem. Implementace níže produkuje AST, který se tvoří ve výstupním zásobníku.

func (p *Parser) Parse(tokenList []*lexer.Token) (ast.Node, error) {
	output := make([]ast.Node, 0)
	opStack := make([]*lexer.Token, 0)
	var err error

tokenLoop:
	for i := 0; i < len(tokenList); i++ {
		curToken := tokenList[i]
		switch curToken.Type() {
		case lexer.Number:
			// if the token is a number, then: push it to the output queue
			output = append(output, ast.NumericNode(curToken.Value()))


		case lexer.Identifier:
			//  if the token is a function then: push it onto the operator stack
			if tokenList[i+1].Type() == lexer.LPar {
				// Expecting the identifier is function name, because is followed by (
				opStack = append(opStack, tokenList[i])
			} else {
				// if the token is a variable name, then: push it to the output queue.
				output = append(output, ast.VariableNode(tokenList[i].Identifier()))
			}


		case lexer.Addition, lexer.Substraction, lexer.Exponent, lexer.Multiplication,
			lexer.Division, lexer.FloorDiv, lexer.Modulus:
			// if the token is an operator then: while there is an operator at the top of the operator stack
			for len(opStack) > 0 {
				topStackEl := opStack[len(opStack)-1]
				if topStackEl.Type() == lexer.LPar {
					break
				}
				// If the operator at the top of the operator stack has greater precedence
				// OR
				// The operator at the top of the operator stack has equal precedence AND the token is left associative
				if p.priorities.GetPrecedence(topStackEl.Type()) > p.priorities.GetPrecedence(curToken.Type()) ||
					(p.priorities.GetPrecedence(topStackEl.Type()) == p.priorities.GetPrecedence(curToken.Type()) &&
						p.priorities.GetAssociativity(curToken.Type()) == parser.LeftAssociativity) {

					// pop operators from the operator stack onto the output queue
					output, err = p.addToOutput(output, topStackEl)
					opStack = opStack[:len(opStack)-1]
					continue
				}
				break
			}
			// push token onto the operator stack
			opStack = append(opStack, curToken)


		case lexer.LPar:
			// if the token is a left parenthesis, then: push it onto the operator stack
			opStack = append(opStack, curToken)


		case lexer.RPar:
			// if the token is a right parenthesis, then:
			// while the operator at the top of the operator stack is not a left parenthesis:
			for len(opStack) > 0 {
				topStackEl := opStack[len(opStack)-1]
				if topStackEl.Type() == lexer.LPar {
					break
				}
				// pop the operator from the operator stack onto the output queue.
				output, err = p.addToOutput(output, topStackEl)
				opStack = opStack[:len(opStack)-1]
			}
			// if there is a left parenthesis at the top of the operator stack, then:
			// pop the operator from the operator stack and discard it
			opStack = opStack[:len(opStack)-1]
			// if there is a function token at the top of the operator stack, then:
			// pop the function from the operator stack onto the output queue.
			if opStack[len(opStack)-1].Type() == lexer.Identifier {
				output, err = p.addToOutput(output, opStack[len(opStack)-1])
				opStack = opStack[:len(opStack)-1]
			}
		}
		if err != nil {
			return nil, err
		}
	}

	// while there are still operator tokens on the stack
	for len(opStack) > 0 {
		// pop the operator from the operator stack onto the output queue
		topStackEl := opStack[len(opStack)-1]
		output, err = p.addToOutput(output, topStackEl)
		opStack = opStack[:len(opStack)-1]
	}
	return opStack, err
}

// addToOutput is converting nodes in output list into a AST

func (p *Parser) addToOutput(output []ast.Node, token *lexer.Token) ([]ast.Node, error) {
	var op ast.Operation
	switch t := token.Type(); t {
	case lexer.UnaryAddition, lexer.UnarySubstraction:
		output[len(output)-1] = ast.NewUnaryNode(t, output[len(output)-1])
	case lexer.Addition, lexer.Substraction, lexer.Multiplication, lexer.Division, lexer.Exponent,
		lexer.FloorDiv, lexer.Modulus:

		r := output[len(output)-1]
		l := output[len(output)-2]
		output = output[:len(output)-1]
		output[len(output)-1] = ast.NewBinaryNode(t, l, r)
	case lexer.Identifier:
		// Current functions support only 1 parameter
		output[len(output)-1] = ast.NewFunctionNode(token.Identifier(), output[len(output)-1])
	}
	return output, nil
}

Úpravy algoritmu a možná rozšíření

Algoritmus výše vychází z pseudokódu na anglické Wikipedii, který ale nebude plně fungovat pro vstupy jako 5 9 88 nebo ++/*--*+/66. Nekontroluje totiž, jestli se po tokenu čísla nebo proměnné nachází operátor a naopak. Nezvládá také zpracovat unární operátory + a - nebo funkce s proměnným počtem parametrů.

První dva problémy jsou vyřešené pomocí proměnné expect. Tato stavová proměnná se přepíná mezi stavy ExpectOperand a ExpectOperator a kontroluje, zda se zpracovává token správného typu. Rozšíření je detailněji popsané na StackOverflow a pomocí této metody lze také rozšířit algoritmus a přidat podporu pro unární operátory.

Rozšíření algoritmu a přidání podpory pro proměnný počet argumentů funkce bude popsáno v jednom z dalších dílů seriálu.

---

S názory na článek nebo algoritmus samotný se můžete podělit v komentářích