Lexer - 1. díl vlastní kalkulačky s výrazy

Article in English can be found on dev.to/arxeiss/lexer-expression-calculator-3j9p

Tento článek patří do seriálu Vlastní kalkulačka s výrazy. Ostatní články seriálu:

• Lexer - 1. díl vlastní kalkulačky s výrazy
• Shunting yard algoritmus - 2. díl vlastní kalkulačky
• Evaluator AST - 3. díl vlastní kalkulačky
• Recursive descent - 4. díl vlastní kalkulačky

---

Možností, jak matematické výrazy zpracovat, je více. Tento seriál se zaměří na implementaci pomocí lexeru, který vstup tokenizuje. A parseru, jehož výstupem bude AST neboli abstraktní syntaktický strom. Parsery zkusím implementovat 2, každý s trochu jiným přístupem.

Na myšlenku zkusit vytvořit vlastní chytrou kalkulačku mě přivedl úkol pro 18. den v AoC 2020.

Lexer a tokeny

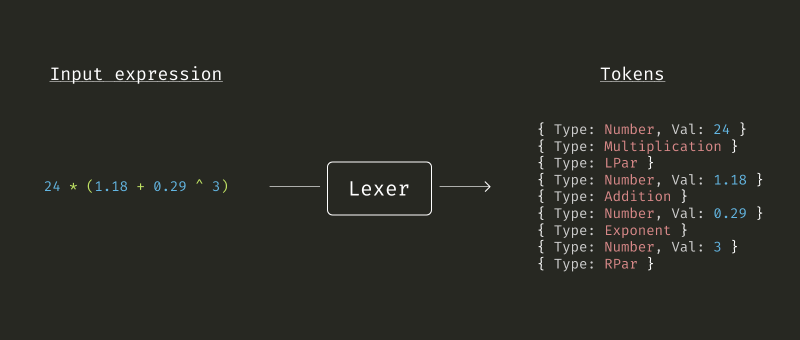
Lexer provádí tzv. lexikální analýzu, což je proces, který převádí vstupní text na sekvenci tokenů. Token má konkrétní význam a může mít i hodnotu. V našem případě bude operátor token bez hodnoty, zatímco číslo bude token s hodnotou. V prvním kroku je nutné si všechny typy podporovaných tokenů definovat. Pro kalkulačku jich moc není, další se časem možná přidají.

Celý kód včetně testů lze nalézt na Githubu v repozitáři arxeiss/go-expression-calculator.

type TokenType uint8

const (
	EOL TokenType = iota // End Of Line
	Unknown
	LPar           // Levá závorka
	RPar           // Pravá závorka
	Exponent       // Mocnina
	Multiplication // Násobení
	Division       // Dělení
	FloorDiv       // Dělení se zaokrouhlením dolů
	Modulus        // Zbytek po dělení
	Addition       // Sčítání
	Substraction   // Odčítání
	Number         // Číslo - token s hodnotou
	Identifier     // Identifikátor - token s hodnotou (pro proměnné a funkce)
	Whitespace     // Bílé znaky, mezery
)



type Token struct {
	tType            TokenType
	value            float64
	idName           string
}

Zjednodušení s regulárními výrazy

Celý proces lexikální analýzy se dá implementovat pomocí konečeného automatu. To je ale dost práce a já raději šáhl po regulárních výrazech. Kromě kódu jej lze nalézt na adrese regex101.com, kde jej budu v případě rozšiřování aktualizovat. Důvod, proč jsem šáhl po regulárních výrazech byl hlavně ten, že chci podporovat zápis čísel v mnoha tvarech. Tedy 123, 5.48, .13, 71.41e2, 9.731e+3, 4.43e-4 a samozřejmě všechny další kombinace těchto zápisů. 

Ukázka Lexeru - zjednodušená verze

Zde je ukázka lexeru ve zjednodušené formě. Pomocí regulárního výrazu se text rozdělí do jednotlivých nálezů, které pak lze převést na dané tokeny. Tento kód ale neošetřuje úplně neznámé znaky, které regulární výraz ignoruje. Celý kód lze nalézt na Githubu včetně testů.

var tokenRegexp = regexp.MustCompile(`\(|\)|\*\*|\^|//|%|\+|\-|\*|/|(?P<num>(?:[0-9]+(?:\.[0-9]+)?|\.[0-9]+)(?:e[+-]?[0-9]+)?)|(?P<id>(?i)[a-z_][a-z0-9_]*)|(?P<ws>\s+)`)

type Lexer struct {
	expr string
}

func NewLexer(expression string) *Lexer {
	return &Lexer{expr: expression}
}

func (l *Lexer) Tokenize() ([]*Token, error) {
	expr := make([]*Token, 0)

	for _, match := range tokenRegexp.FindAllStringSubmatch(l.expr, -1) {
		t := &Token{}
		switch {
		case match[2] != "":
			t.tType = Identifier
			t.idName = match[2]
		case match[1] != "":
			t.tType = Number
			var err error
			if t.value, err = strconv.ParseFloat(match[1], 64); err != nil {
				return nil, TokenError(t, ErrInvalidNumber)
			}
		case match[3] != "": // Ignore whitespace for now and skip it
			continue
		default:
			t.tType = operatorTokenType(match[0])
		}
		expr = append(expr, t)
	}
	expr = append(expr, &Token{tType: EOL})
	return expr, nil
}


func operatorTokenType(operator string) TokenType {
	switch operator {
	case "(":
		return LPar
	case ")":
		return RPar
	case "^", "**":
		return Exponent
	case "*":
		return Multiplication
	case "/":
		return Division
	case "//":
		return FloorDiv
	case "%":
		return Modulus
	case "+":
		return Addition
	case "-":
		return Substraction
	}
	return Unknown
}

Proč potřebujeme tokeny?

Proč se řeší nějaké tokeny, proč bude celý kód rozdělen na lexer, parser a možná i další části? Samozřejmě, že by vše šlo udělat najednou. Vše je o nějaký zaběhlých principech, jako je například Single-responsibility principle, který spadá do SOLID. Lexer má jenom úlohu zpracovat text a vytvořit z něj tokeny. Parser poté převede tokeny na AST.

Kdyby vzešel požadavek, aby kalkulačka uměla zpracovat vstup jako je tento 5 PLUS 8 TIMES 4 stačilo by přepsat pouze lexer. Pokud by se nerozšířila gramatika, nebyl by důvod zasahovat do dalších částí programu.

---

Pokud vás článek zaujal, doporučuji přečíst si celou sérii. A nezapomeňte zanechat komentář.